The concept of machine pervades our culture, and has occupied an important place in philosophical debates for at least the last two or three centuries.
For example, it is often argued that living organisms, or the human mind, are "ultimately just machines". I.e. underlying all the organic, often amorphous complexity of the world we perceive, is a level at which ultra-miniscule machines function predictably. Electrons spinning around nuclei at an exact, measurable speed; light photons traveling always at a particular speed. At the heart of biological processes are DNA molecules whose properties can in theory be exactly deduced from the sequence of molecules of which they consist.
But if "everything is a machine", we could stop using the word because it doesn't distinguish anything from anything else.
For many words, like "fish", "atom", "electron", "planet", "star", one can readily settle on a canonical technical or scientific definition, but for "machine" this does not seem to be true, so it seems like a word that is best understood by its common usage.
In common usage, "machine" refers to a man-made object the exact size, shape, and other properties of whose parts are precisely determined (often, it is said they are constructed by "precise machining") which will behave, or respond to manipulation, in precise ways (unless something breaks).
In nature, it is hard to find anything that quite looks like this. To find mechanical behavior ready-to-hand in nature (before books, economic systems, large-scale governments, and factories came into being), we have to start with systems simpler than what we normally think of as a machine. A good example is a rock that is thrown. Once set in motion, there is such predictability about the trajectory of the rock that a skilled person can make it strike in a certain place from 100 feet away.
In prehistoric times, when hand-throwing of projectiles (e.g. rocks, spears) was an essential skill, it was a great mystery what went on between
(1) the moment when I think of hitting "that animal with this rock" and
(2) the moment when the rock leaves my hand in flight towards the animal.
How does the thought lead to the perfect motion of the hand? Even today, we only have sketchy explanations.
But with the rock (or cannon ball) in motion itself, the mysteries have long since solved by the study of trajectories. In the renaissance, men like da Vinci and Galileo developed mathematical theories for modeling these trajectories, and successfully used these theories to calculate the elevation of a cannon's muzzle that will make the ball land on the target.
The path of the cannonball, as science tells us today, is so simple and predictable because forces have been isolated. We can almost say that the rock's path is determined by (1) its initial velocity and (2) the earth's gravity, and the interplay between these two "inputs" is indeed simple, and reducible to a formula, as Newton showed.
Now the caveman could not work out this theory; nevertheless the mathematically predictable behavior of a compact heavy object in flight (given its velocity and direction at the moment it goes into free flight) made it possible for the right-brain, which deals with spatial relations in a nonverbal way, to determine how to throw a rock in order to hit a target. We know there is another complicating force, wind resistence, but it is strongest with light objects like feathers, and negligible, to a useful approximation for compact heavy bodies.
When we build a machine, we build something such that the dominant forces affecting any part are extremely simple, and ones we can control. Forces like friction, usually in conflict with our design goals, are minimized partly through using polished, precisely straight or precisely round, or otherwise precisely, regularly, fashioned surfaces, and arrangements. Once set in motion, we know which way our mechanical contraption will go; or if we want it to go a certain way, we know how to make this happen. Where do we find anything of such regularity in nature?
The rock or cannonball in flight is one such. Being a system that only exists for a second, it may not seem very satisfactory. Yet much of what Galileo learned about nature came from studying such trivial mechanical systems as a compact body in passive free flight.
For millennia, we have had the stars and planets to look at. Their combination of mostly ultra-simple regularity, with the exception of a handful of objects called planets (Latin for "wanderers") tantalized humans, who correctly guessed that to understand them might solve a great and important mystery. Hoping to solve a mystery with a strong direct bearing on our lives, they produced various forms of astrology, and believed that comets, among the rarest and least regular phenomena foretold disasters. Over several millennia, some people have intuited that the night sky, with its thousands of visible points always fixed in the same relative position, and the moon and 5 planets which followed their own more mysterious rules, and the sun which rendered most of the rest invisible, gestured towards some important solvable mystery, and this was one of the earliest examples of good scientific thinking.
In the 17th century, it was finally persuasively shown that this night sky disclosed one of the first great natural machines ever comprehended by mankind. A set of bodies in motion, so arranged that all the possible forces that could come into play have been put into a balance, such that only some few properties determine the visible parts of the system's functioning
Perhaps we should really study the idea of mechanical regularity, how humankind ever discovered such a thing (which may help us understand something about how the idea is construed by people). What sorts of things we can accomplish with this phenomenon called mechanical regularity, and to what extent does it really pervade nature.
Before the solar system could be seen in its true shape, time had to become more real and measurable. The idea of a second, and that each day consisted of 86,400 of them, would have been incoherent until a few centuries ago. For millennia the measurement of physical length or distance played an indispensable role in technology, facilitating the building of large structures such as bridges, castles, and cathedrals. True measurability of time, however, was hardly dreamt of. Ultimately the key to the measurability of time was to map time onto distance.
The necessary thing was a machine that always moved at the same speed. This had to be difficult. Without seconds and minutes, how do you even define speed? The significance of the pendulum was, like so many other things, first described by Galileo. Its significance was that a well designed pendulum could go on swinging back and forth for days, and even though the distance of the swing decreased over time, the length of time for each swing remains almost exactly the same. To explain this in terms of physics is quite complex. The formula given by Wikipedia is:
The usefulness of a well constructed pendulum was discovered long before this complex formula could be guessed at or justified by physics, but it produced a very simple regularity -- with a pendulum of the right length, one swing = one second (or some precise number of seconds, even as the swing of the pendulum gets shorter throughout the day. And the use of gears can make a clock's second hand and other hands travel at a very nearly constant speed, mapping time onto the distance traveled by the hands.
Mechanical regularity is a rare phenomenon in nature, or in anything we can easily construct from nature. We have to look very hard to find it, and in doing so, we develop a habit of not focusing on the contingent.
If our surroundings seem very regular and controllable, as they do in our very technological world, it is not just because humankind "discovered" the regularities of nature. It is largely because we rearranged the substances of our world into regular, governable, objects.
[Note: The next and final couple of paragraphs are ruminations that haven't gotten very far, and may appear to point in directions that I would disavow after spending more time with them:]
During the Enlightenment, there was a great fascination with the idea of social engineering. But what do we have to do to make people and societies controllable? We make objects controllable by isolating and simplifying the relevant forces, eliminating those that are irregular or that we don't understand by purifying the materials; making things exactly round or exactly straight or exactly flat (as nearly as possible).
One an analogous process with human beings is to reduce motivations to one simple one, which, for someone in the right position, can be easy to manipulate; i.e. fear. Or it could be money.
At any rate, that is largely the rule that slave owners followed, and the rule used by the largest-scale social engineers of the last two centuries: Napoleon, Hitler, and the leaders of the large Communist nations.
The liberal economists had a different approach. They had no desire for, and abhorred a totalizing (for a nation or world) social machine that would perform acrobatics and turn on a dime. But they helped provide a lens for looking at humankind strictly through its relationship with money -- very attractive as it is all reducible to numbers, raising the hope of powerful physics-like formulas. There is indeed the enticement that all our efforts might be reduced to an optimization problem to be solved by a computer.

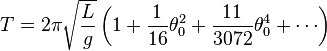



No comments:
Post a Comment